[백준/C++] 15649번 : N과 M(1)

우선 완전탐색이란 무엇인가 부터 알아봤다. 

 

완전탐색이란?

 

모든 경우의 수를 다 따져가며 찾는 방식이라고 한다. 즉 어떤 답을 찾기 위해 n번의 시도를 해야된다면, 그 n번을 다 훑어서 맞는지 아닌지 찾는 느낌이다. 그래서 시간복잡도는 O(n)이다. 그래서 오래걸리는 편이기 때문에, 시간제한을 보고 가능한지 판단해야된다고 한다.

 

예를들어, 시간제한이 1초가 걸려있다. 1초엔 1억번의 계산만 가능하므로, 만약 10억번의 연산이 필요한 문제라면 완전탐색 알고리즘을 쓸 경우 시간오버가 된다한다. 그래서 문제를 풀 땐, 시간 복잡도를 계산하고 이를 기반으로 완전탐색이 가능한지 판단해야된다!\

 

백트레킹이란?

 

모든 경우의 수를 탐색하다 만약 조건에 맞지 않으면 그 즉시 중단하고 이전으로 돌아가여 다시 확인하는 것을 반복하면서 원하는 조건을 찾는 알고리즘이다. 완전탐색 유형 중 하나인듯하다. 백트레킹은 재귀함수로 푸는 방식이 다수인 듯 하다.

 

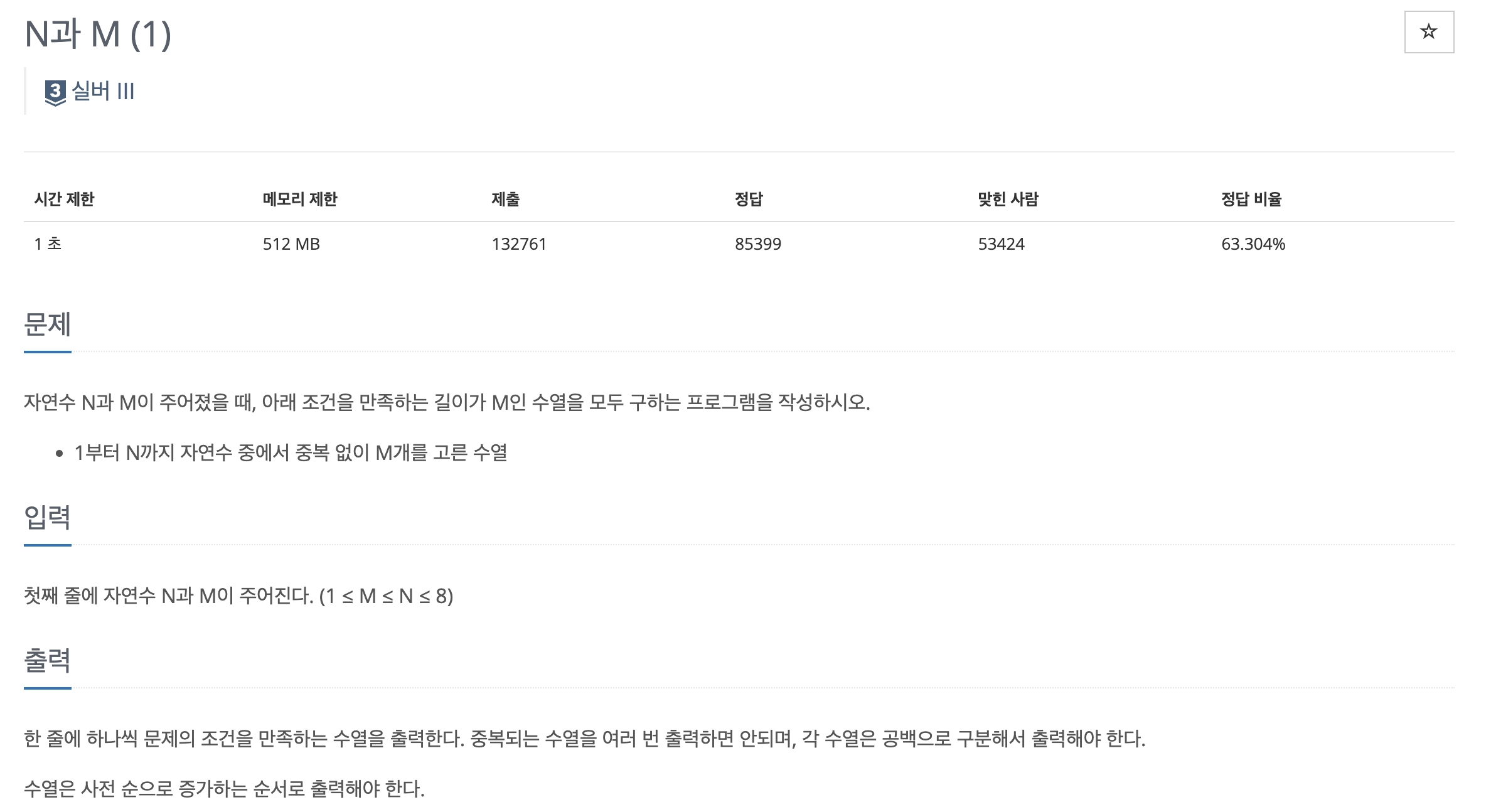
이때 길이가 들어오는 수에 따라 달라지므로, 중첩반복문은 되게 코드낭비가 심할것같다. 재귀로 풀어보자. 아래 코드를 봐보자

#include <iostream>
using namespace std;

int N, M;
bool visited[9];  // 방문 여부 체크 (1~8까지 사용)
int arr[9];       // 선택한 숫자 저장

void backtrack(int depth) {
    if (depth == M) {  // M개의 숫자를 선택했으면 출력
        for (int i = 0; i < M; i++) {
            cout << arr[i] << " ";
        }
        cout << "\n";
        return;
    }

    for (int i = 1; i <= N; i++) {
        if (!visited[i]) {  // 아직 사용하지 않은 숫자라면 선택
            visited[i] = true;
            arr[depth] = i;  // 현재 숫자 저장
            backtrack(depth + 1);  // 다음 숫자 선택
            visited[i] = false;  // 백트래킹 (원상 복구)
        }
    }
}

int main() {
    cin >> N >> M;
    backtrack(0);
    return 0;
}

 

재귀함수를 통해, 길이가 M인 배열에 사용 여부를 판단하면서 숫자를 하나씩 넣을 것이다. 방문여부체크는 visited배열을 통해 관리한다. 이렇게 재귀를 쓰면, 간단하게 풀이 가능하다!